Background
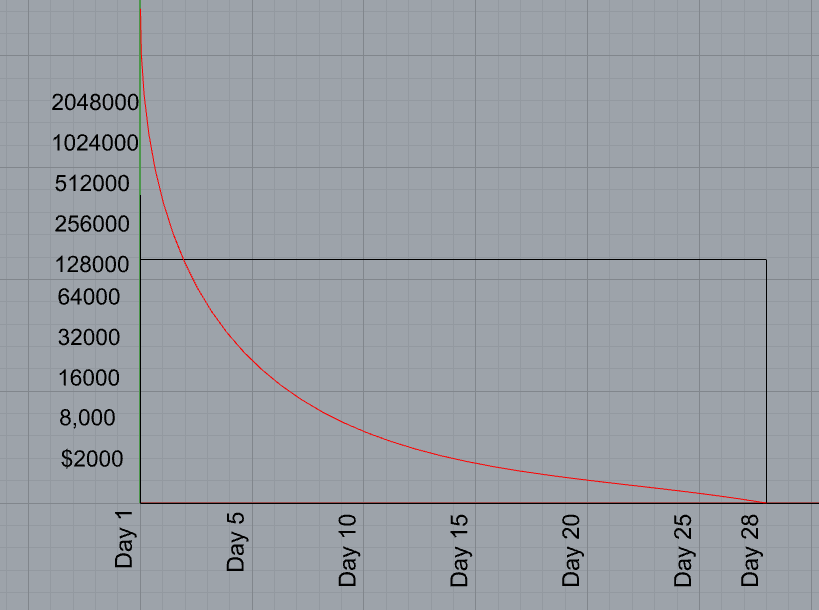
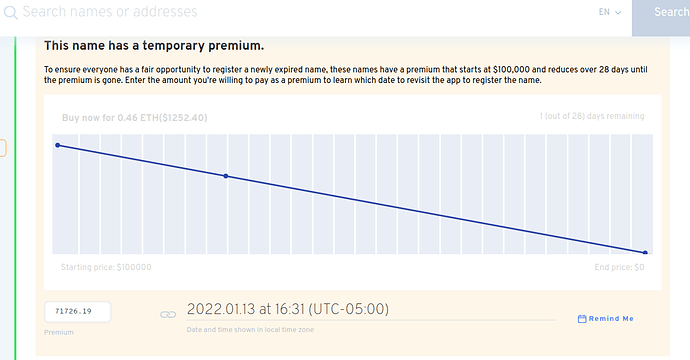
The ENS registrar controller uses a price premium contract to calculate the premium of a name, which decays to 0 over 28 days. This uses a linear price function and has historically been $2000 up until recently when many names have been sniped and was changed in EP5 to $100k: [EP5] [Executable] Set the temporary premium start price to $100,000
This is probably as high as we can go for linear based pricing curve as the price will start to decay very quickly as you increase the price. E.g. at $100k over 28 days, that is already $3571 a day or $148 an hour. While that isn’t the worst, if we increase the price to $1m over 28 days, it’ll decrease at $1480 an hour, which would provide pretty bad UX for someone trying to buy a name at a specific price.
We have already had someone snipe a 3 letter name at $100k. In a dutch auction ideally we don’t want anyone to be able to buy the name at the top price otherwise the auction itself is not functioning properly. However with a linear function, to further increase the start price would decrease user experience in one of 2 ways. Either the price drops too quickly or the name will be in this auction for a much longer period of time, which is also a bad user experience. Therefore all things considered, an exponential price curve could be a better solution.
The initial price curve we have discussed is reducing the price by 50% per day, which can be expressed as the following equation:
Price = StartPrice * 0.5 ^ Days
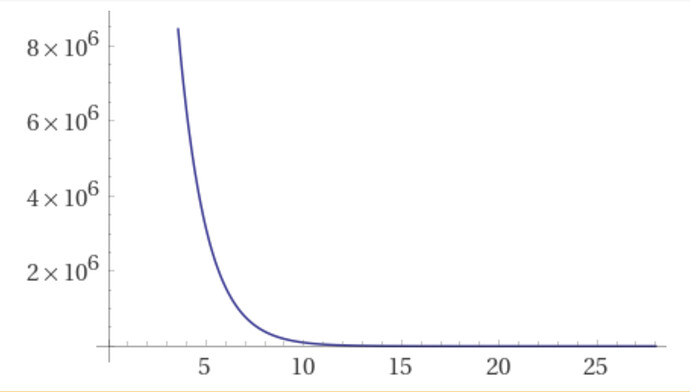
This would create a price graph like this:
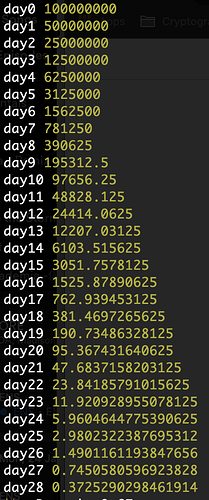
With a starting price of $100m, the price would drop to $3 mil in 5 days, $100k in 10 days, $100 in 20 days and $.0.37 in 28 days.
Here is the list of prices from day 0 to day 28:
As you can see after the initial high prices, the premium price has a much more manageable decrease in price
Implementation
To efficiently implement this in solidity, we needed a way to do floating point exponentiation in Solidity. Since this isn’t possible, the only way we could do it is fixed point exponentiation, but this means to get meaningful precision for something like 0.5^25.56 (25 days with 2 decimal precision) , we’d have to do 5^2556, which would give us a number with almost 2000 digits in it, which would overflow in the EVM. Therefore to represent the fractional part of the days with a reasonable amount of accuracy, we precomputed values using JavaScript and hardcoded these in a lookup table that would allow us to compute the exponents using much smaller numbers. The hardcoded lookup table gives us 16 bit precision, which can represent an accurate price every ~1.3 seconds, which is accurate enough for our use case.
For the whole days, we can then just right shift the number to get a cheap divide by 2. E.g. for 3 days we right shift by 3. For 3.5 days, we right shift by 3 and then calculate the fractional exponent using our table and combine them.
Finally to create a smooth transition to 0 premium after 28 days, we take the final value, which is around $0.37 and minus that from the value when calculating, so instead of having the price start at $100m and end at $0.37, we start at ($100m - $0.37) and end at 0.
The PR for the contract is available here:
From my benchmarks, the function takes around 30k gas. And if you’re wondering why it’s not in an array and looped rather than a bunch of if statements, it’s because we can’t make arrays constants in solidity yet, so it saves about 5k gas.
I’d appreciate any feedback on the implementation.
And thanks to @nick.eth for all the ideas for an efficient implementation.